| Home | Module 1 | Module 2 | Tutorials | Credits | Contact Us |
<<Back to the Previous Page <<Fundamentals <<Knowledgebase Fundamentals |
||||||||||||||||||||
Temperature Effects and Stress Due to Temperature Change As we know, for any material changes in temperature result in volume change. An increase or decrease in temperature results in the expansion or contraction of a structure. To better understand this phenomenon, consider a steel wire with a length,
The increase in the length, In this equation,
As can be seen from the above table, aluminum has larger If the structure is prevented from movements (restrained) while subjected to a temperature change, stresses will develop. Consider the same piece of wire used before with both ends restrained undergoing a temperature rise of
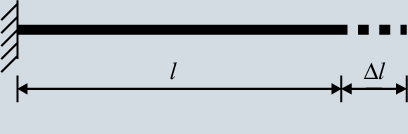
To find how much these stresses are and what parameters they depend on, we first consider the wire without one of the end supports subjected to a temperature increase of
Now, we push the right end of the wire to go back to its original length. This is the force that would have developed in the wire if both ends were restrained when the temperature was raised.
As we know, the stress,
or
The above equation shows the relationship between the changes in temperature and the stress developed in the restrained structure. For aluminum and steel spatial structures undergoing extremely large temperature variations this may become an important issue to consider. However, in most typical cases of spatial structures the temperature effect may be neglected since the developed stresses are negligible.
|
||||||||||||||||||||
© 2011 Virginia Polytechnic Institute and State University
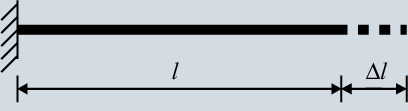
 depends on the material type. The following shows the values of
depends on the material type. The following shows the values of 
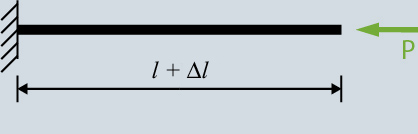
 (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6)